Question

a worker A finishes a project on his own in 12 days. the worker completes the same work alone in 16 days. the two workers started working together, but after 3 days A leaves and B. continues on his own. How many days will B need to finish the rest of the work?

Answer 1

Worker B needs 9 days to finish the rest of the work

Explanation:

Proportions

Worker A finishes a project on his own in 12 days and worker B does the same in 16 days.

Worker A does 1/12 of the project in one day and worker B does 1/16 of the project in one day. When working together, they do

`(1)/(12)+(1)/(16)=(7)/(48)`

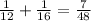
After 3 days they have completed:

`3*(7)/(48)=(7)/(16)`

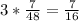
parts of the project, this means it still remains:

`1-(7)/(16)=(9)/(16)`

parts of the project and it is done by B alone. Since B does
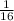`(1)/(16)` per day, he now takes

`\displaystyle ((9)/(16))/((1)/(16))=9`

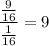
days to complete the project.

Worker B needs 9 days to finish the rest of the work