Answer:
We can say that the end behaviour of polynomial is increasing going up if x is positive or negative,
Explanation:
We need to find the end behaviour of
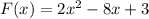
For finding the end behaviour we need to find the degree of polynomial.
Degree of Polynomial:
The term with the largest exponent is termed as degree of polynomial.
Finding degree of polynomial:
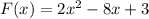
So, the term with largest exponent is 2x^2, so the degree is 2
The dgeree of polynomial is even.
When the degree of polynomial is even, if we plug positive values in x and approaches to ∞ aur function F(x) also approaches to ∞
i.e. if x --> ∞ F(x) --> ∞
Now, if we plug negative values in x and approaches to -∞ our function F(x) also approaches to ∞
i.e. if x --> -∞ F(x) --> ∞
So, we can say that the end behaviour of polynomial is increasing going up if x is positive or negative,
It can be understood by the graph attached