Question

Baseball fans can buy tickets for seats in the lower deck or upper deck of the stadium. Tickets

for the lower deck cost $42 each. Ticket prices for the upper deck are 75% of the cost of
tickets for the lower deck. Which inequality represents all possible combinations of x, the
number of tickets for the lower deck, and y, the number of tidets for the upper deck, that
someone can buy for no more than $800?
A 42x + 56y < 800
B 42% + 31.5y < 800
C 42x + 56y > 800
D 42x + 31.5y > 800​

Answer 1

Answer (corrected option):

B 42x + 31.5y < 800

Explanation:

Inequalities

Inequality is a relationship between variables in which the left side is not equal to the right side. Relational symbols include greater than, different of, less or equal then, etc.

We are told that tickets for the lower deck of a baseball stadium cost $42 each. We are also told the ticket for the upper deck cost 75% of the tickets for the lower deck. We compute 75% $42=$31.50.

Let's say that x is the number of tickets for the lower deck, and y is the number of tickets for the upper deck. The total cost is

42x+31.5y

If someone must pay no more than $800, then

`42x+31.5y \leq 800`

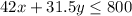
The meaning of 'no more than' also includes limit number 800. That is why we included it in the answer, but all the options don't, so we'll adjust to

`42x+31.5y < 800`

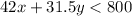
The only option close to the answer is the second one, but it has an inaccuracy. We'll pick it conditioned to be the proposed answer