Question

If a quadratic equation has a discriminant that equals zero, which of the following statements is always true?

a. The equation has two solutions and the parabola will open upward.
b. The equation has one solution and the parabola will open downward.
c. The equation has zero solutions and there is not enough information to determine the direction of the parabola.
d. The equation has one solution and there is not enough information to determine the direction of the parabola.

Answer 1

d. The equation has one solution and there is not enough information to determine the direction of the parabola.

Explanation:

For a general quadratic equation

y = ax² +bx +c

the solution is

`x = (-b\pm√(b^2-4ac))/(2a)`

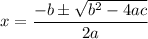
The discriminant (D) is the part of the quadratic formula underneath the radical: b² - 4ac.

D tells us whether there are

• two different real solutions
• two identical real solutions ("one solution")
• two complex solutions.

If D= 0,

`x = (-b)/(2a)\pm0 = \mathbf{(-b)/(2a)}`

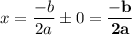
and there are two identical solutions ("one solution").

The direction of the parabola depends on the sign of a.

That information is not given, so we cannot determine the direction of the parabola.