Question

A random sample of 100 people was taken. Eighty of the people in the sample favored Candidate A.

We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 75%.

At a .05 level of significance, it can be concluded that the proportion of the population in favor of candidate A is _____.

a. not significantly greater than 80%

b. significantly greater than 75%

c. not significantly greater than 75%

d. significantly greater than 80%

Answer 1

C

Explanation:

Given:

Number of samples, n = 100

let number of sample that favoured candidate A be x = 80

probability, p' = x/n = 80/100 = 0.8

probability, p for significance = 75% = 0.75

Using Z-proportion test statistics, we have

Z =
`(p' - p)/√(p(1 - p)/n)`

Substituting the values, we have

Z =
`(0.8 - 0.75)/√(0.75(1 - 0.75)/100)`

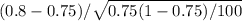
Z = 0.05 / 0.0433 = 1.1547

The p-value is

P(Z>1.1547) = 1 - P(Z≤1.1547)

Checking the Z-score table, P(Z≤1.1547) = 0.8789

Hence, we have 1 - 0.8789

= 0.1241

Hence, the p-value is greater than 0.05, so we cannot say it is very significant.

Hence, the population in favour of candidate A is not significantly greater than 75%