A triangle has side lengths of 7 inches, 12 inches, and c inches. Enter values to write an inequality that describes the possible values for c, the length of the third side of the triangle.
Answer:
The inequality is:
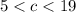
Length of third side "c" can have values greater than 5 but less than 19
Solution:
Given that,
Length of two sides of triangle are 7 inches and 12 inches respectively
Let the length of third side be "c"
The Triangle Inequality Theorem, states that, the sum of the lengths of any two sides of a triangle is greater than the length of the third side
So we get a inequality as:
Case 1:
Sum of length of two sides of triangle > length of third side

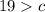
Rewrite,
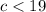
Case 2:
Let 12 inches be the length of third side
Sum of sides of length 7 and c > 12
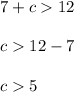
Therefore from case 1 and case 2,
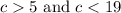
Which can be combined,
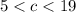
Therefore the possible values of "c" are:
"c" can have values greater than 5 but less than 19