Question

There is a total of $39.55. There are 3 times as many dimes as nickels, how many of each coin type was collected ?

Answer 1

Number of dimes collected is 339 and number of nickels collected is 113

Solution:

Given that There is a total of $39.55

There are 3 times as many dimes as nickels

To find: Number of dimes and nickels collected

Let "d" be the number of dimes collected

Let "n" be the number of nickels collected

We know that,

1 dime = $ 0.10

1 nickel = $ 0.05

From given information,

There are 3 times as many dimes as nickels

So, we get

Number of dimes = 3(number of nickels)

d = 3n

Given that there is total of $ 39.55

number of dimes collected x value of 1 dime + number of nickels collected x value of 1 nickel = $ 39.55

`3n * 0.10 + n * 0.05 = 39.55\\\\0.3n + 0.05n = 39.55\\\\0.35n = 39.55\\\\n = (39.55)/(0.35)\\\\n = 113`

Substitute n = 113 in d = 3n

`d = 3(113) = 339`

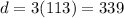
Summarizing the results:

number of dimes collected = 339

number of nickels collected = 113