Answer:
 in
in
Explanation:
Let x be the side of square.
Length of box=8-2x
Width of box=15-2x
Height of box=x
Volume of box=
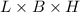
Substitute the values then we get
Volume of box=V(x)=


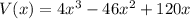
Differentiate w.r.t x
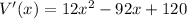
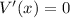
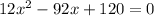
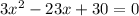
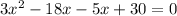

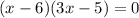
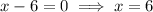
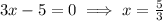
Again differentiate w.r.t x
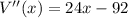
Substitute x=6
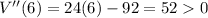
Substitute x=5/3
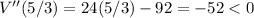
Hence, the volume is maximum at x=

Therefore, the side of the square ,
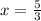 in cutout that gives the box the largest possible volume.
in cutout that gives the box the largest possible volume.