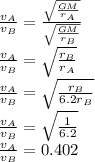Question

Planet A and planet B are in circular orbits around a distant star.

Planet A is 6.2 times farther from the star than is planet B.

What is the ratio of their speeds vA/vB?

Express your answer using three significant figures.

Answer 1

`(v_A)/(v_B)=0.402`

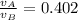
Step-by-step explanation:

The speed that planets must have in order for their orbit to be stable, is given by:

`v=\sqrt{(GM)/(r)}`

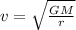
Here v It is called orbital speed, G is the gravitational constant, M is the mass of the star and r is the radius of the orbit. In this case we have:

`r_A=6.2r_B`

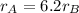
So, the ratio of their speed is:

`(v_A)/(v_B)=\frac{\sqrt{(GM)/(r_A)}}{\sqrt{(GM)/(r_B)}}\\(v_A)/(v_B)=\sqrt{(r_B)/(r_A)}\\(v_A)/(v_B)=\sqrt{(r_B)/(6.2r_B)}\\(v_A)/(v_B)=\sqrt{(1)/(6.2)}\\(v_A)/(v_B)=0.402`