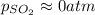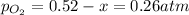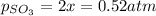Answer:
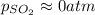
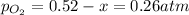
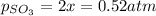
Step-by-step explanation:
The equilibrium system is defined by:

First of all, we need to be given the equilibrium constant for this reaction. Equilibrium constant is temperature-dependent. For the purpose of this problem and illustration of the thought process, we'll assume room temperature for which the equilibrium constant of this reaction is defined as:
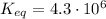
Define the equilibrium constant in terms of equilibrium molarities:
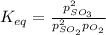
Let's say that x atm of oxygen react, then, according to stoichiometry, 2x atm of sulfur dioxide react and 2x atm of sulfur trioxide are formed. The equilibrium amounts are then:
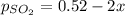

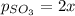
Substitute into the K expression:

For such a huge equilibrium constant, we may assume that this reaction nearly goes to completion, so we'd have a limiting reactant, in which:

This means:
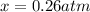
And the equilibrium partial pressures become: