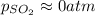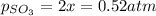Question

2 SO2(g) + O2(g) equilibrium reaction arrow 2 SO3(g) Calculate the equilibrium partial pressures of SO2, O2, and SO3 produced from an initial mixture in which the partial pressures of SO2 and O2 = 0.52 atm and the partial pressure of SO3 = 0 (exactly).

Answer 1

`p_(SO_2) \approx 0 atm`

`p_(O_2) = 0.52 - x = 0.26 atm`

`p_(SO_3) = 2x = 0.52 atm`

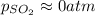
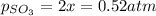
Step-by-step explanation:

The equilibrium system is defined by:

`2 SO_2 (g) + O_2 (g)\rightleftharpoons 2 SO_3 (g)`

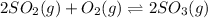
First of all, we need to be given the equilibrium constant for this reaction. Equilibrium constant is temperature-dependent. For the purpose of this problem and illustration of the thought process, we'll assume room temperature for which the equilibrium constant of this reaction is defined as:

`K_(eq) = 4.3\cdot 10^6`

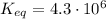
Define the equilibrium constant in terms of equilibrium molarities:

`K_(eq) = (p_(SO_3)^2)/(p_(SO_2)^2p_(O_2))`

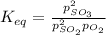
Let's say that x atm of oxygen react, then, according to stoichiometry, 2x atm of sulfur dioxide react and 2x atm of sulfur trioxide are formed. The equilibrium amounts are then:

`p_(SO_2) = 0.52 - 2x`

`p_(O_2) = 0.52 - x`

`p_(SO_3) = 2x`

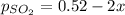
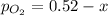
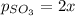
Substitute into the K expression:

`K_(eq) = 4.3\cdot 10^6 = ((2x)^2)/((0.52 - 2x)^2(0.52 - x))`

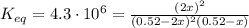
For such a huge equilibrium constant, we may assume that this reaction nearly goes to completion, so we'd have a limiting reactant, in which:

`0.52 - 2x\approx 0`

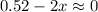
This means:

`x = 0.26 atm`

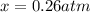
And the equilibrium partial pressures become:

`p_(SO_2) \approx 0 atm`

`p_(O_2) = 0.52 - x = 0.26 atm`

`p_(SO_3) = 2x = 0.52 atm`