Answer:
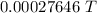

-0.04194 V
Step-by-step explanation:
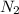 = Number of turns in outer solenoid = 330
= Number of turns in outer solenoid = 330
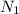 = Number of turns in inner solenoid = 22
= Number of turns in inner solenoid = 22
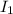 = Current in inner solenoid = 0.14 A
= Current in inner solenoid = 0.14 A
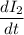 = Rate of change of current = 1800 A/s
= Rate of change of current = 1800 A/s
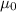 = Vacuum permeability =
= Vacuum permeability =
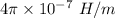
r = Radius = 0.0115 m
Magnetic field is given by
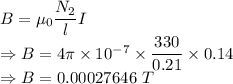
The average magnetic flux through each turn of the inner solenoid is
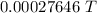
Magnetic flux is given by

Mutual inductance is given by
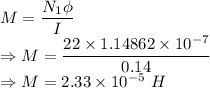
The mutual inductance of the two solenoids is

Induced emf is given by

The emf induced in the outer solenoid by the changing current inthe inner solenoid is -0.04194 V