Answer:
Shown Below
Explanation:
The question says:
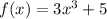
![g(x)=\sqrt[3]{(x-5)/(3)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9r760y9dvfzqlzcsvrodfweihpf67k3u6p.png)
And it says to verify that both functions are inverses of each other.
To show this, we have to understand one composition of function property. When 2 functions are inverses of each other, the composition of both functions should yield "x". In notation:
(f o g)(x) = f(g(x)) = x
and
(g o f)(x) = g(f(x)) = x
So, we need to show that putting f(x) into g(x) and putting g(x) into f(x) both yields "x". Lets show this:
First:
![(fog)(x)=f(g(x))=3(\sqrt[3]{(x-5)/(3)} )^3+5=3((x-5)/(3))+5=x-5+5=x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qfbma1ggel7p5imj7bqs2rnrt5c85yucz5.png)
Verified.
Second:
![(gof)(x)=g(f(x))=\sqrt[3]{((3x^3+5)-5)/(3)}=\sqrt[3]{(3x^3)/(3)}=\sqrt[3]{x^3} =x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wg6d6xa0my4vsecp6dcspj1nm493bejdz5.png)
Verified.
We have shown that both the functions are inverse of each other.