Answer:
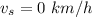

Step-by-step explanation:
Relative Speed
A boat traveling in still waters has a speed v_b. If now an opposite stream appears, then the apparent speed of the boat will be less than before because the relative speed is the subtraction of both speeds. Thus we say
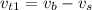
Conversely, if the stream goes with the boat, both speeds are added.
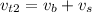
where
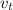 it the total or real speed of the boat respect to the ground,
it the total or real speed of the boat respect to the ground,
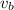 is the speed of the boat in still water, and
is the speed of the boat in still water, and
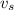 is the speed of the stream.
is the speed of the stream.
The boat goes 36 km with stream. The time it took for doing so is:
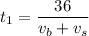
The boat goes 24 km against the stream in
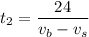
The problem states that
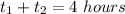
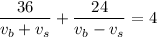
Knowing
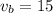
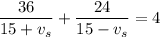
Operating
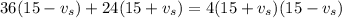
Rearranging and simplifying

Factoring
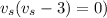
We get
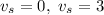
Both solutions are possible, i.e.
1. The stream does not exist and the boat travels the total distance of 60 Km in 4 hours
2. The stream has a speed of 3 Km/h and the boat travels 36 km in 2 hours and 24 km in 2 hours