Question

In a simple random sample of 1000 Americans, it was found that 61% were satisfied with the service provided by the dealer from which they bought their car. In a simple random sample of 1000 Canadians, 58% said that they were satisfied with the service provided by their car dealer. Which of the following statements concerning the sampling variability of these statistics is true? a. larger for the Canadians because the sample size is smaller.

b. smaller for the sample of Canadians, since the population of Canada is less than half that of the United States. Hence, the sample is a larger proportion of the population.

c. smaller for the sample of Canadians, since the percentage satisfied was smaller than that for the Americans.

d. larger for the Canadians, since Canadian citizens are more widely dispersed throughout their country than American citizens are in the United States. Hence, Canadians have more variable views.

Explain your answer

Answer 1

The correct option is a)

larger for the Canadians because the sample size is smaller.

Explanation:

Using the formula for finding the variation of proportion

S.d= √(p×q)/n

P= 0.61 q= 1- 0.61= 0.39 n= 1000

S.d= √(0.61×0.39)/1000

S.d= 0.0154 sampling variability for American

P= 0.58 q= 0.42 n= 1000

S.d= √(p×q)/n

S.d= √(0.58×0.42)/1000

S.d= 0.0156 sampling variability for Canadians

Therefore the sampling variability is

larger for the Canadians because the sample size is smaller.

Answer 2

c. smaller for the sample of Canadians, since the percentage satisfied was smaller than that for the Americans.

Correct we see that the proportion of Canadians is lower than the proportion of Americans since 0.58<0.61. And the reason why is by the percentage.

Explanation:

Data given and notation

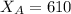`X_(A)=610` represent the number of people of America satisfied

`X_(C)=580` represent the number of people of Canada satisfied

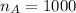`n_(A)=1000` sample of Americans selected

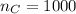`n_(C)=1000` sample of Canadians selected

`p_(A)=(610)/(1000)=0.61` represent the proportion of American people satisifed

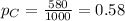`p_(C)=(580)/(1000)=0.58` represent the proportion of Canadians satisfied

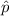`\hat p` represent the pooled estimate of p

Solution to the problem

If we analyze one by one the optiosn we have this:

a. larger for the Canadians because the sample size is smaller.

False, both have the same the same sample size of 1000 and the proportion of Canadians is less than the proportion of Americans.

b. smaller for the sample of Canadians, since the population of Canada is less than half that of the United States. Hence, the sample is a larger proportion of the population.

False, the proportion of Canada is not less than half of the United States since the difference is just 0.61-0.58=0.03

c. smaller for the sample of Canadians, since the percentage satisfied was smaller than that for the Americans.

Correct we see that the proportion of Canadians is lower than the proportion of Americans since 0.58<0.61. And the reason why is by the percentage.

d. larger for the Canadians, since Canadian citizens are more widely dispersed throughout their country than American citizens are in the United States. Hence, Canadians have more variable views.

False the porportion of Canadians 0.58 is NOT higher than the proportion of Americans satisfied 0.61 since 0.58 is not less than 0.61.