Answer:
The central angle measure of the sector divided by the total angle measure of a circle multiplied by the area of the circle will yield the area of the sector
Explanation:
we know that
The formula to calculate the area of sector is equal to
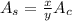
where
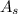 ----> is the area of sector
----> is the area of sector
 ----> is the central angle measure of the sector in degrees
----> is the central angle measure of the sector in degrees
 ---> total angle measure of a circle in degrees
---> total angle measure of a circle in degrees
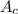 ---> represent the area of the circle
---> represent the area of the circle
see the attached figure to better understand the problem
we have
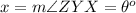 ----> central angle of sector ZYX
----> central angle of sector ZYX
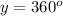 ----> total angle measure of a circle in degrees
----> total angle measure of a circle in degrees
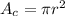 ---> represent the area of the circle
---> represent the area of the circle
substitute in the formula
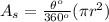
therefore
The central angle measure of the sector divided by the total angle measure of a circle multiplied by the area of the circle will yield the area of the sector