Question

In the figure, angle ZYX is measured in degrees. The area

of the shaded sector can be determined using the formula
Which best explains the formula?
m ZZYX (nr?).
360°
The central angle measure of the sector divided
total angle measure of a circle multiplied by the a
the circle will yield the area of the sector.
The central angle measure of the sector divided
total angle measure of a circle multiplied by the
circumference of the circle will yield the area of the
sector
The central angle measure of the sector multiplied
the area of the circle will yield the area of the secton
The central angle measure of the sector multiplied
the circumference of the circle will yield the area oft
sector
Mark this and return
Save and Exit
Next
Submit

Answer 1

the answer is A on e2020

Explanation:

Answer 2

The central angle measure of the sector divided by the total angle measure of a circle multiplied by the area of the circle will yield the area of the sector

Explanation:

we know that

The formula to calculate the area of sector is equal to

`A_s=(x)/(y)A_c`

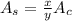
where

`A_s` ----> is the area of sector

`x` ----> is the central angle measure of the sector in degrees

`y` ---> total angle measure of a circle in degrees

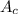`A_c` ---> represent the area of the circle

see the attached figure to better understand the problem

we have

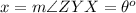`x=m\angle ZYX=\theta^o` ----> central angle of sector ZYX

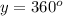`y=360^o` ----> total angle measure of a circle in degrees

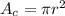`A_c=\pi r^(2)` ---> represent the area of the circle

substitute in the formula

`A_s=(\theta^o)/(360^o) (\pi r^(2))`

therefore

The central angle measure of the sector divided by the total angle measure of a circle multiplied by the area of the circle will yield the area of the sector