Question

Use the fundamental definition of a derivative to find f'(x) where f(x)=
`(x+a)/(x+b)`

The answer I get is
`(-a+b)/(\left(x+b\right)^(2))` , but I'm not entirely sure if this is correct and also I'm not sure if I'm using the right method.

Answer 1

(b-a)/(x+b)²

Explanation:

f(x+h) = (x+h+a)/(x+h+b)

limit h -->0

[f(x+h) - f(x)]/h

(x+h+a)/(x+h+b) - (x+a)/(x+b)

[(x+b)(x+h+a) - (x+h+b)(x+a)] ÷ [h(x+h+b)(x+b)]

[x²+xb+hx+hb+ax+ab-x²-ax-hx-ha-bx-ab] ÷ [h(x+h+b)(x+b)]

[bh - ah] ÷ [h(x+h+b)(x+b)]

h(b-a) ÷ [h(x+h+b)(x+b)]

(b-a) ÷ [(x+h+b)(x+b)]

As h --> 0

(b-a)/(x+b)²

Answer 2

Yes, you are right.

See explanation.

Explanation:

The definition of derivative is:

`f'(x)=\lim_(h \rightarrow 0) (f(x+h)-f(x))/(h)`.

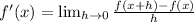We are given
`f(x)=(x+a)/(x+b)`.

Assume
`a \text{ and } b` are constants.

If
`f(x)=(x+a)/(x+b)` then
`f(x+h)=((x+h)+a)/((x+h)+b)`.

Let's plug them into our definition above:

`f'(x)=\lim_(h \rightarrow 0) (f(x+h)-f(x))/(h)`

`f'(x)=\lim_(h \rightarrow 0) (((x+h)+a)/((x+h)+b)-(x+a)/(x+b))/(h)`

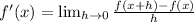
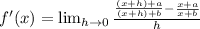
I'm going to find a common denominator for the main fraction's numerator.

That is, I'm going to multiply first fraction by
`1=(x+b)/(x+b)` and

I'm going to multiply second fraction by
`1=((x+h)+b)/((x+h)+b)`.

This gives me:

`f'(x)=\lim_(h \rightarrow 0) ((((x+h)+a)(x+b))/(((x+h)+b)(x+b))-((x+a)((x+h)+b))/((x+b)((x+h)+b)))/(h)`

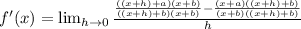
Now we can combine the fractions in the numerator:

`f'(x)=\lim_(h \rightarrow 0) ((((x+h)+a)(x+b)-(x+a)((x+h)+b))/(((x+h)+b)(x+b)))/(h)`

I'm going to multiply a bit on top and see if there is anything than can be canceled:

`f'(x)=\lim_(h \rightarrow 0) (((x+h)x+(x+h)b+ax+ab-x(x+h)-xb-a(x+h)-ab)/(((x+h)+b)(x+b)))/(h)`

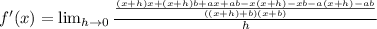
Note: I do see that
`(x+h)x-x(x+h)=0`.

I also see
`ab-ab=0`.

I will also distributive in other places in the mini-fraction's numerator.

`f'(x)=\lim_(h \rightarrow 0) ((xb+bh+ax-xb-ax-ah)/(((x+h)+b)(x+b)))/(h)`

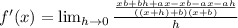
Note: I see
`xb-xb=0`.

I also see
`ax-ax=0`.

`f'(x)=\lim_(h \rightarrow 0) ((bh-ah)/(((x+h)+b)(x+b)))/(h)`

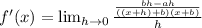
In the numerator of the mini-fraction on top the two terms contain a factor of
`h` so I can factor that out.

This will give me something to cancel out across the main fraction since
`(h)/(h)=1`.

`f'(x)=\lim_(h \rightarrow 0) ((h(b-a))/(((x+h)+b)(x+b)))/(h)`

`f'(x)=\lim_(h \rightarrow 0) (((b-a))/(((x+h)+b)(x+b)))/(1)`

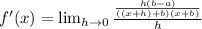
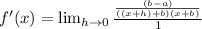
So we now have gotten rid of what would make this over 0 if we had replace
`h` with 0.

So now to evaluate the limit, that is also we have to do now.

`(((b-a))/(((x+0)+b)(x+b)))/(1)`

`((b-a))/(((x)+b)(x+b)))/(1)`

`(((b-a))/((x+b)(x+b)))/(1)`

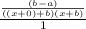
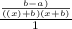
I'm going to go ahead and rewrite this so that isn't over 1 anymore because we don't need the division over 1.

`(b-a)/((x+b)(x+b))`

`(b-a)/((x+b)^2)`

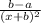
or what you wrote:

`(-a+b)/((x+b)^2)`