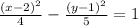Question

HELP ASAP:

Write an equation of hyperbola with foci at (-1, 1) and (5, 1) and vertices at (0, 1) and (4, 1)

Answer 1

The answer to your question is

`((x - 2)^(2) )/(4) - ((y - 1)^(2))/(5) = 1`

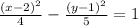
Explanation:

Data

Foci (-1, 1) and (5, 1) [A and B]

Vertices (0, 1) and (4, 1) [C and D]

See the image below. From the image we can conclude that it is a horizontal hyperbola.

Equation

`((x - h)^(2) )/(a^(2) ) - ((y - k)^(2) )/(b^(2) ) = 1`

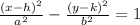
From the image calculate the center

The center is in the middle of the vertices (2, 1)

Now, calculate a, a is the distance from the center to the vertices, a = 2

Calculate c, c is the distance from the center to the foci, c = 3

Calculate b with the pythagorean theorem c² = a² + b²

b² = c² - a²

b² = 3² - 2²

b² = 9 - 4

b² = 5

Substitution

`((x - 2)^(2) )/(4) - ((y - 1)^(2))/(5) = 1`