Question

Find the area of a square with the given length of its side.

3 1/2a^3

Answer 1

`A=(12(1)/(4))(a^(6))\ units^2`

Explanation:

we know that

The area of a square is equal to

`A=b^(2)`

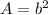
where

b is the length side of the square

In this problem we have

`b=(3(1)/(2))a^(3)\ units`

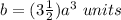
Convert mixed number to an improper fraction

`3(1)/(2)=(3*2+1)/(2)=(7)/(2)`

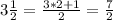
substitute

`b=(7)/(2)a^(3)\ units`

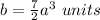
substitute in the formula of area

`A=((7)/(2)a^(3))^(2)`

`A=((7)/(2))^2(a^(3))^(2)`

`A=((49)/(4))(a^(3*2))`

`A=((49)/(4))(a^(6))\ units^2`

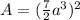
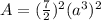
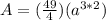
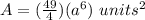
Convert 49/4 to mixed number

`(49)/(4)=(48)/(4)+(1)/(4)=12(1)/(4)`

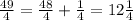
substitute

`A=(12(1)/(4))(a^(6))\ units^2`