Question

What are the roots of the polynomial equation?

x2−14x−32=0

Enter your answers in the boxes.
x1=
x2=

Answer 1

shorter answer is

x1= -2

x2= 16

Answer 2

Explanation:

Factor this the "old fashoined" way. In our polynomial, which is a quadratic,

a = 1, b = -14, c = -32

a * c --> 1 * -32 = -32

The factors of 32:

1, 32

2, 16

4, 8

The only 2 factors that combine to give us our b value of -14 are 2 and 16, as long as we make the 16 negative. 16 + 2 = -14. Filling in to rewrite our quadratic,

`x^2-16x+2x-32`

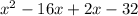
Now group them together in groups of 2:

`(x^2-16x)+(2x-32)`

Out of the first set of parenthesis we can factor out an x, and out of the second set of parenthesis we can factor out a 2:

`x(x-16)+2(x-16)`

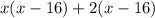
What's common now is the (x - 16) which can be factored out, leaving us with

(x - 16)(x + 2)

That means that

x = 16 and x = -2