Question

Find an equation of the line passing through the given points. Write the equation in the function notation.

(3,4) and (4,1)

F(x)=

Answer 1

straight line equation

known two points namely (3,4) and (4,1)

the formula looking for equations if known two points is

`(x2 - x1)/(x1 - x) = (y2 - y1)/(y1 - y)`

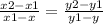
You can enter the numbers provided above into the formula

`(x2 - x1)/(x1 - x) = (y2 - y1)/(y1 - y) \\ (4 - 3)/(3 - x) = (1 - 4)/(4 - y) \\ (1)/(3 - x) = ( - 3)/(4 - y) \\ - 9 + 3x = 4 - y \\ y = - 3x + 13`

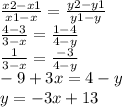
You can check the function is true or false

(3,4) 3=x and 4=y

y = -3(3) + 13

y = -9 + 13

y = 4 ✔️

*additional :

y = -3x + 19 ===== f(x) = -3x + 19

Answer 2

First you need to find the slope of the line using the given coordinates of the two points.
The slope of the line = (1-4)/(4-3) = -3
Then you choose one pair of the coordinates given, either (3,4) or (4,1) , up to you, to find the equation of the line.
If you choose (3,4)
Then
(y-4)/(x-3) = -3
(y-4) = -3x+9
y = -3x+13

If you choose (4,1),
Then
(y-1)/(x-4) = -3
y-1 = -3x+12
y = -3x+13

So, F(x)=-3x+13