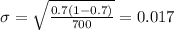Answer:
C.Approximately normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis greater than or equals 10.np(1−p)≥10.
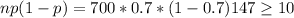
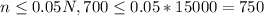
And as we can see we satisfy both so the normal approximation on this case would be appropiate.
1) The mean of the sampling distribution for the estimated proportion correspond to the population proportion parameter, in other words:
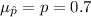
Since it's an unbiased estimator for the population proportion.
2) The standard deviation is given by this formula:
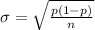
And if we replace we got:
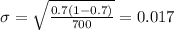
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The population proportion have the following distribution
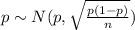
Solution to the problem
C.Approximately normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis greater than or equals 10.np(1−p)≥10.
In order to apprximate the distribution with the normal distribution we need to satisfy two basic conditions given by:
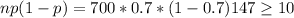
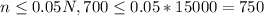
And as we can see we satisfy both so the normal approximation on this case would be appropiate
Part 1
The mean of the sampling distribution for the estimated proportion correspond to the population proportion parameter, in other words:
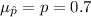
Since it's an unbiased estimator for the population proportion.
Part 2
The standard deviation is given by this formula:
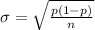
And if we replace we got: