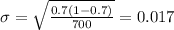Question

Describe the sampling distribution of ModifyingAbove p with caretp. Assume the size of the population is 15 comma 00015,000.n=700​, p=0.70

A.Not normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis less than 10.np(1−p)<10.
B.Not normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis greater than or equals 10.np(1−p)≥10.
C.Approximately normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis greater than or equals 10.np(1−p)≥10.
D.Approximately normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis less than 10.np(1−p)<10.

1. Determine the mean of the sampling distribution of ModifyingAbove p with caretp.mu Subscript ModifyingAbove p with caret Baseline equalsμp=nothing
(Round to one decimal place as​ needed.)

2. Determine the standard deviation of the sampling distribution of ModifyingAbove p with caretp.sigma Subscript ModifyingAbove p with caret Baseline equalsσp=nothing
(Round to three decimal places as​ needed.)

Answer 1

C.Approximately normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis greater than or equals 10.np(1−p)≥10.

`np(1-p)=700*0.7*(1-0.7)147 \geq 10`

`n \leq 0.05 N , 700 \leq 0.05*15000=750`

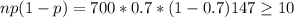
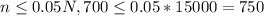
And as we can see we satisfy both so the normal approximation on this case would be appropiate.

1) The mean of the sampling distribution for the estimated proportion correspond to the population proportion parameter, in other words:

`\mu_(\hat p) = p =0.7`

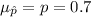
Since it's an unbiased estimator for the population proportion.

2) The standard deviation is given by this formula:

`\sigma= \sqrt{(p(1-p))/(n)}`

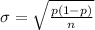
And if we replace we got:

`\sigma= \sqrt{(0.7(1-0.7))/(700)}=0.017`

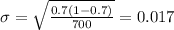
Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

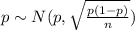
Solution to the problem

C.Approximately normal because n less than or equals 0.05 Upper Nn≤0.05N and np left parenthesis 1 minus p right parenthesis greater than or equals 10.np(1−p)≥10.

In order to apprximate the distribution with the normal distribution we need to satisfy two basic conditions given by:

`np(1-p)=700*0.7*(1-0.7)147 \geq 10`

`n \leq 0.05 N , 700 \leq 0.05*15000=750`

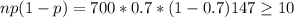
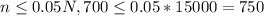
And as we can see we satisfy both so the normal approximation on this case would be appropiate

Part 1

The mean of the sampling distribution for the estimated proportion correspond to the population proportion parameter, in other words:

`\mu_(\hat p) = p =0.7`

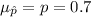
Since it's an unbiased estimator for the population proportion.

Part 2

The standard deviation is given by this formula:

`\sigma= \sqrt{(p(1-p))/(n)}`

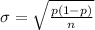
And if we replace we got:

`\sigma= \sqrt{(0.7(1-0.7))/(700)}=0.017`