Answer:
1)
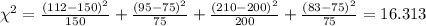
2)
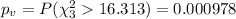
And we got the same decision reject the null hypothesis at 5% of significance.
Explanation:
Previous concepts
The Chi-Square test of independence is used "to determine if there is a significant relationship between two nominal (categorical) variables". And is defined with the following statistic:
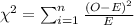
Where O rpresent the observed values and E the expected values.
State the null and alternative hypothesis
Null hypothesis: The distribution is 30% catfish, 15% bass, 40% bluegill, and 15% pike
Alternative hypothesis: The distribution is NOT 30% catfish, 15% bass, 40% bluegill, and 15% pike
The observed values are given by the table given:
Catfish =112, BAss = 95, Bluegill=210, Pike=83
Calculate the expected values
In order to calculate the expected values we can use the following formula for each cell of the table
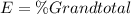
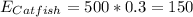
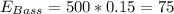
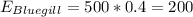
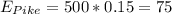
Part 1: Calculate the statistic
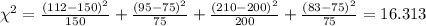
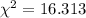
Calculate the critical value
First we need to calculate the degrees of freedom given by:

Since the confidence provided is 95% the significance would be
 and we can find the critical value with the following excel code: "=CHISQ.INV(0.95,3)", and our critical value would be
and we can find the critical value with the following excel code: "=CHISQ.INV(0.95,3)", and our critical value would be
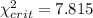
We can calculate also the p value:
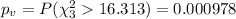
And we got the same decision reject the null hypothesis at 5% of significance.