Question

Suppose that profit for a particular product is calculated using the linear equation: Profit = 20S + 3D. Which of the following combinations of S and D would yield a maximum profit?

a. S = 0, D = 0
b. S = 405, D = 0
c. S = 0, D = 299
d. S = 182, D = 145

Answer 1

b. S = 405, D = 0

Explanation:

We have been given that profit for a particular product is calculated using the linear equation:
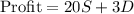`\text{Profit}=20S+3D`. We are asked to choose the combinations of S and D that would yield a maximum profit.

To solve our given problem, we will substitute given values of S and D in the profit function one by one.

a. S = 0, D = 0

`\text{Profit}=20S+3D`

`\text{Profit}=20(0)+3(0)`

`\text{Profit}=0`

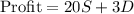
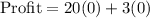
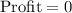
b. S = 405, D = 0

`\text{Profit}=20S+3D`

`\text{Profit}=20(405)+3(0)`

`\text{Profit}=8100+0`

`\text{Profit}=8100`

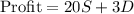
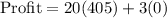
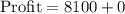
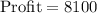
c. S = 0, D = 299

`\text{Profit}=20S+3D`

`\text{Profit}=20(0)+3(299)`

`\text{Profit}=0+897`

`\text{Profit}=897`

d. S = 182, D = 145

`\text{Profit}=20S+3D`

`\text{Profit}=20(182)+3(145)`

`\text{Profit}=3640+435`

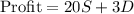
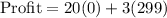
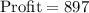
`\text{Profit}=4075`

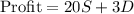
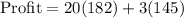
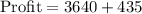
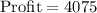
Since the combination S = 405, D = 0 gives the maximum profit ($8100), therefore, option 'b' is the correct choice.