Answer:
The pickup truck and hatchback will meet again at 440.896 m
Step-by-step explanation:
Let us assume that both vehicles are at origin at the start means initial position is zero i.e.
 = 0. Both the vehicles will cross each other at same time so we will make equations for both and will solve for time.
= 0. Both the vehicles will cross each other at same time so we will make equations for both and will solve for time.
Truck:
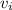 = 33.2 m/s, a = 0 (since the velocity is constant),
= 33.2 m/s, a = 0 (since the velocity is constant),
 = 0
= 0
Using
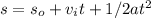
s = 33.2t .......... eq (1)
Hatchback:
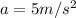 ,
,
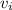 = 0 m/s (since initial velocity is zero),
= 0 m/s (since initial velocity is zero),
 = 0
= 0
Using
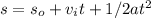
putting in the data we will get
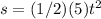
now putting 's' value from eq (1)
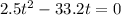
which will give,
t = 13.28 s
so both vehicles will meet up gain after 13.28 sec.
putting t = 13.28 in eq (1) will give
s = 440.896 m
So, both vehicles will meet up again at 440.896 m.