1 Answer

Ask a Question

Shmulik · Answer 1 · 2020-02-26T06:21:51+0000

Answer:

a) True b) False c) True

Explanation:

a). When using the shell method, the axis of the cylindrical shells is parallel to the axis of revolution. (True)

The axis of the cylindrical shell is always parallel to its axis of revolution, whether it is vertical or horizontal. When we're using the Shell Method. (Check the graph below)

Vertical Axis of Revolution:

$\int_(a)^(b)2 \pi xf(x) dx$

Horizontal Axis of Revolution:

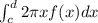
$\int_(c)^(d)2 \pi xf(x) dx$

b) If a region is revolved about the y-axis, then the shell method must be used.

False. This is not the determining factor to choose the method. We can calculate the volume of a Solid of Revolution around the y-axis by the Disk Method, for instance.

In the case below, we can calculate the Volume using the the Disk Method.

Calculate the Volume of Solid by the region delimited by

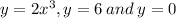
$y=2x^(3), y=6 \:and\: y=0$

$V=\int_(0)^(6) \pi xf(x) dx\\A(y)=\pi \left ( \sqrt[3]{(y)/(2)}\right )^(2) \Rightarrow A(y)=\left ( (y)/(2) \right )^{(2)/(3)}\\V=\int_(0)^(6)\pi\left ( (y)/(2) \right )^{(2)/(3)}\ dy \\V=\frac{3\pi\sqrt[3]{6}}{5\sqrt[3]{4}}\approx 23.53 u^(3)$

c) If a region is revolved about the x-axis, then in principle it is possible to use the disk/washer method and integrate with respect to x or the shell method and integrate with respect to y.

True.

This is a matter of convenience. In some cases, if we prefer calculate by the Shell Method with respect to y instead, of doing this by the Disk Method we'd fall into a very hard situation, because some calculations are very difficult or even impossible.

Example:

Calculate the volume of

$y=1-(x^(2))/(16)\:, [-4,4]$

By the Disk Method:

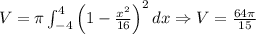
$V=\pi\int_(-4)^(4)\left ( 1-(x^(2))/(16) \right )^(2) dx\Rightarrow V=(64\pi)/(15)$

By the Shell:

1) Solve for x

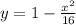
y=1-(x^(2))/(16)

2) Evaluate an "udu" Integral

3) Integrate it with respect to y (...) no to x

Clearly the Disk Method is more convenient