Question

2. Suppose that an isosceles right triangle is slowly expanding outwards with both legs of the triangle increasing at a rate of 10 cm/min. At the moment that the legs are 2 cm, how fast is the hypotenuse increasing in length? Fully simplify your answer

Answer 1

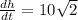`(dh)/(dt)=10√(2)`=14.14 [cm/min]

Step-by-step explanation:

If we have an isosceles right triangle we can use the Pythagoras theorem to find the hypotenuse:

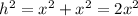`h^(2)=x^(2)+x^(2)=2x^(2)` (1)

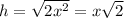`h=\sqrt{2x^(2)}=x√(2)` (2)

From equation (2) let's take the derivative with respect to time (t):

`\frac {dh}{dt}=\frac {dx(\sqrt {2})}{dt}`

`\frac {dh}{dt}=\frac {dx}{dt}\sqrt {2}`

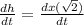
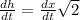
dx/dt is the increasing rate of the triangle legs, it is dx/dt = 10 [cm/min].

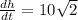`(dh)/(dt)=10√(2)`=14.14 [cm/min] (3)

(3) is the hypotenuse increasing in length, and when x = 2 cm, using equation (2), h will be equal to 2.83 cm.

Hava a nice day!