Question

A 0.4000 kg sample of methanol at 16.0ºC is mixed with 0.4000 kg of water at 85.0ºC. Assuming no heat loss to the surroundings, what is the final temperature of the mixture? The specific heat of methanol is 2450 J/kg•ºC, the specific heat capacity of liquid water is 4180 J/kg⋅°C

Answer 1

T_finalmix = 59.5 [°C].

Step-by-step explanation:

In order to solve this problem, a thermal balance must be performed, where the heat is transferred from water to methanol, at the end the temperature of the water and methanol must be equal once the thermal balance is achieved.

`Q_(water)=Q_(methanol)`

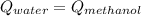
where:

`Q_(water)=m_(water)*Cp_(water)*(T_(waterinitial)-T_(final))`

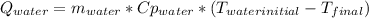
mwater = mass of the water = 0.4 [kg]

Cp_water = specific heat of the water = 4180 [J/kg*°C]

T_waterinitial = initial temperature of the water = 85 [°C]

T_finalmix = final temperature of the mix [°C]

`Q_(methanol)=m_(methanol)*Cp_(methanol)*(T_(final)-T_(initialmethanol))`

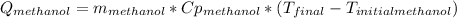
Now replacing:

`0.4*4180*(85-T_(final))=0.4*2450*(T_(final)-16)\\142120-1672*T_(final)=980*T_(final)-15680\\157800=2652*T_(final)\\T_(final)=59.5[C]`