Answer:
54.6 m/s^2
Step-by-step explanation:
length of the pendulum, l = 1 m
time period of the pendulum, T = 0.85 s
According to the formula of time period of pendulum
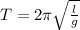
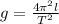
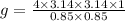
g = 54.6 m/s^2
Thus, the acceleration due to gravity at this planet is 54.6 m/s^2.