Question

The children between ages of 2 and 5 watch an average of 25 hours of TV per week. Assume that standard deviation is 3 hours of TV per week, if a sample 20 children between ages of 2-5 are randomly selected with the mean sample of 26.3. Find the probability that the mean number of hours they watch TV is greater than 2.6 hours.

Answer 1

the probability that the mean number of hours they watch TV is greater than 26.3 hours is 0.034

Explanation:

Last part of the question is wrong. It should be:

Find the probability that the mean number of hours they watch TV is greater than 26.3 hours.

P('the mean number of hours the children between ages of 2 and 5 watch TV' >26.3 hours) = P(t>t*) where

t* is the t-score of 26.3 hours. It can be found using the equation:

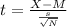`t=(X-M)/((s)/(√(N) ) )` where

• X =26.3 hours

• M is the mean number of hours the children between ages of 2 and 5 watch TV (25 hours)

• s is the standard deviation (3 hours)

• N is the sample size (20)

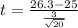`t=(26.3-25)/((3)/(√(20) ) )`: ≈1.938

Corresponding p-value with 19 degrees of freedom: P(t>1.938) is ≈ 0.034