Question

Find the electric field at a point in the z axis for a charge distribution of 4 point charges of magnitude Q located at (d,0,0), (-d,0,0), (0,-d,0) and (0,d,0). (The coordinates are expressed in a Cartesian coordinate system.)

Answer 1

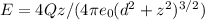`E=4Qz/(4\pi e_(0) (d^(2)+z^(2))^(3/2))` in the z direction is the electric field at a point in the z axis for a given charge distribution.

Step-by-step explanation:

Even before we begin the actual calculation we have to note the symmetry of the charge distribution. If the charge on the z axis is held fixed then we note that, for every charge on either x or y axis there is an equal charge present in the negative part of the axis same distance away from the center. If we draw out the geometry of the situation we will see that the x component of the field on the charge on the z axis from the charge on the positive x-axis will cancel the x component of the field from the negative x-axis, so we will be left with just the z component of the field, since the force on the charge on the z axis is repulsive and upwards. We also see that the y component of the field on the charge on the z axis from the charge on the positive y-axis will cancel the y component of the field from the charge from the negative y-axis as well, so again we will be left with just the z component of the field pointing upward since the force on the charge on the z axis is repulsive and upwards. We can write down the field on the charge explicitly by adding the vector electric field contributions from the 4 charges(Using electric field formula derived from columbs law for each charge given below),

`E=Q/4\pi e_(0)r^2`

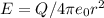
Just the magnitude. if you multiply this by the unit vector in the direction of the electric field, we get the electric field vector. We see the cancellation happen mathematically like below,

`E = Q*(-di+zk)/(4\pi e_(0)(d^2 + z^2)^(3/2) ) +Q*(di+zk)/(4\pi e_(0)(d^2 + z^2)^(3/2) ) +Q*(-dj+zk)/(4\pi e_(0)(d^2 + z^2)^(3/2) ) +Q*(dj+zk)/(4\pi e_(0)(d^2 + z^2)^(3/2) )`

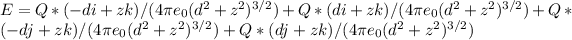
The magnitude of the electric field is the same from all four charges as shown by the 4 terms above, only their direction changes as shown. If we just simplify by adding the components we obtain,

`E=4Qz.k/(4\pi e_(0) (d^(2)+z^(2))^(3/2))`

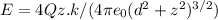
The electric field. The direction of the field is upward(since the electric field vector contains only k the unit vector in the z direction.) because of the reasoning above and the mathematical simplification in the second last equation whereby the x components and the y components of the field at the point z on the z-axis cancel out due to the symmetrical distribution of the charges.