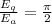Answer:
Step-by-step explanation:
Assuming this problem: "Part (a) of the figure attached shows a non-conducting rod with a uniformly distributed charge +Q. The rod forms a half circle with radius R and produces an electric field of magnitude Earc at its center of curvature P. If the arc is collapsed to a point at distance R from P (Figure b), by what factor is the magnitude of the electric field at P multiplied?"
On this case the charge density is given by this formula:
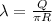 assuming a half circle
assuming a half circle
We can find the force acting on the x axis with this:
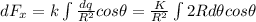
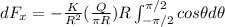
We can cnvert the integral using the symmetrical property:

And we can find the electric field like this:
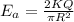
And the electric field just by the charge is given by:
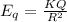
And if we find the ratio for the two electrical fields we got: