Answer:
E=Ur/2E_{0}
Step-by-step explanation:
Consider a long cylindrical charge distribution of radius R with a uniform charge density rho. (a) Find the electric field at distance r from the axis where r R.
to find the electric point inside the cylinder
r=radius of the cylinder
A=curved surface area of the cylinder
∪=charge density
Q=is the net charge
V=volume of the cylinder
Q=UV
volume of the gaussian cylinder =
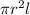
Q=
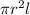 U
U
area A=
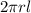
Write the expression Gaussian law
∅=∫EdA=Q/
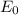 ..........................1
..........................1
E_{0} is the permittivity of free space and Eois the electric field
rewriting the equation 1 , we have
EA=Q/E_{0}
substituting for A and also for Volume V in the equation above
E*
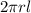 =
=
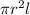 U/E_{0}
U/E_{0}
E=Ur/2E_{0}