Question

Consider a long cylindrical charge distribution of radius R with a uniform charge density rho. (a) Find the electric field at distance r from the axis where r R.

Answer 1

E=Ur/2E_{0}

Step-by-step explanation:

Consider a long cylindrical charge distribution of radius R with a uniform charge density rho. (a) Find the electric field at distance r from the axis where r R.

to find the electric point inside the cylinder

r=radius of the cylinder

A=curved surface area of the cylinder

∪=charge density

Q=is the net charge

V=volume of the cylinder

Q=UV

volume of the gaussian cylinder =
`\pi r^(2) l`

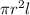
Q=
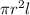`\pi r^(2) l`U

area A=
`2\pi rl`

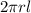
Write the expression Gaussian law

∅=∫EdA=Q/
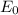`E_(0)`..........................1

E_{0} is the permittivity of free space and Eois the electric field

rewriting the equation 1 , we have

EA=Q/E_{0}

substituting for A and also for Volume V in the equation above

E*
`2\pi rl`=
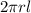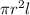`\pi r^(2) l`U/E_{0}

E=Ur/2E_{0}