Question

The moons of Mars, Phobos (Fear) and Deimos (Terror), are very close to the planet compared to Earth's Moon. Their orbital radii are 9,378 km and 23,459 km respectively. What is the ratio of the period of revolution of Phobos to that of Deimos?

Answer 1

`0.2528`

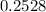
Step-by-step explanation:

To calculate the period we need the formula:

`T=(2\pi r^(3/2))/(√(GM))`

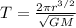
Where
`r` is the radius of the moon,
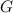`G` is the universal constant of gravitation and
`M` is the mass of mars.

The period of Phobos:

`T_(p)=(2\pi r_(p)^(3/2))/(√(GM))`

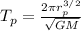
The period of Deimos:

`T_(D)=(2\pi r_(D)^(3/2))/(√(GM))`

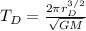
The ratio of the period of Phobos and Deimos:

`(T_(p))/(T_(D))=((2\pi r_(p)^(3/2))/(√(GM)))/((2\pi r_(D)^(3/2))/(√(GM)))`

`(T_(p))/(T_(D))=(√(GM)2\pi r_(p)^(3/2))/(√(GM)2\pi r_(D)^(3/2))`

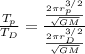
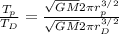
Most terms get canceled and we have:

`(T_(p))/(T_(D))=(r_(p)^(3/2))/(r_(D)^(3/2))`

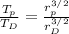
According to the problem

`r_(p)=9,378km\\r_(D)=23,459km`

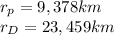
so the ratio will be:

`(T_(p))/(T_(D))=((9,378)^(3/2))/((23,459)^(3/2))=(908166.22)/(3593058.125)=0.25275` ≈
`0.2528`

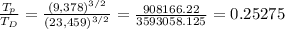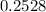
the ratio of the period of revolution of Phobos to that of Deimos is 0.2528