Answer:
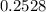
Step-by-step explanation:
To calculate the period we need the formula:
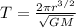
Where
 is the radius of the moon,
is the radius of the moon,
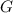 is the universal constant of gravitation and
is the universal constant of gravitation and
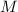 is the mass of mars.
is the mass of mars.
The period of Phobos:
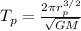
The period of Deimos:
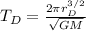
The ratio of the period of Phobos and Deimos:
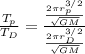
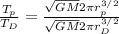
Most terms get canceled and we have:
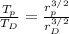
According to the problem
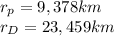
so the ratio will be:
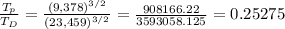 ≈
≈
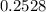
the ratio of the period of revolution of Phobos to that of Deimos is 0.2528