Question

As part of a study done for a large corporation, psychologists asked randomly selected employees to solve a collection of simple puzzles while listening to soothing music. Twenty-three (23) out of 56 employees solved the puzzles in less than 7 minutes. Suppose an employee in the study is selected randomly. Calculate the probability that they take longer than 7 minutes to solve the puzzles.

Answer 1

`P(A')=1-0.411=0.589`

And that represent the probability that they take longer than 7 minutes to solve the puzzles.

Explanation:

The complement rule is a theorem that provides a connection between the probability of an event and the probability of the complement of the event. Lat A the event of interest and A' the complement. The rule is defined by:
`P(A)+P(A') =1`

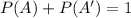
On this case we have that n= 56 represent the employees selected to solve the puzzles.

We know that 23 out of the 56 selected solved the puzzles in less than 7 minutes.

Let's define the events A and A' like this:

A: Employees solved puzzles in less than 7 minutes

By the complement rule then:

A' : Employees solved puzzles in more than 7 minutes

Based on this we are interested to find the probability for A'

We can begin finding P(A), from the definition of probability we know:

`P(A)=(Possible outcomes)/(Total outcomes)`

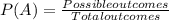
For this case if we replace we got:

`P(A) =(23)/(56)=0.411`

And using the complemnt rule we got:

`0.411 +P(A')=1`

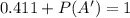
And solving for P(A') we got:

`P(A')=1-0.411=0.589`

And that represent the probability that they take longer than 7 minutes to solve the puzzles.