Question

A continuous random variable, X, whose probability density function is given by f(x) = ( λe−λx , if x ≥ 0 0, otherwise is said to be an exponential random variable with parameter λ denoted by X ∼ Exp(λ) where λ > 0.

(a) Find the c.d.f of X.
(b) Suppose that the length of a phone call in minutes is an exponential random variable with parameter λ = 1 10 . If someone arrives immediately ahead of you at a public telephone booth, find the probability that you will have to wait between 10 and 20 minutes

Answer 1

a)
`F(x) = \lambda \int_0^(\infty) e^(-\lambda x) dx= -e^(-\lambda x) \Big|_0^(\infty) = 1- e^(-\lambda x) \`

b)
`P(10 < X<20)=e^(-0.1*10) -e^(-0.1*20)=0.368-0.135=0.233`

Step-by-step explanation:

Previous concepts

The cumulative distribution function (CDF) F(x),"describes the probability that a random variableX with a given probability distribution will be found at a value less than or equal to x".

The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate). It is a particular case of the gamma distribution".

Part a

Let X the random variable of interest. We know on this case that
`X\sim Exp(\lambda)`

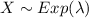
And we know the probability denisty function for x given by:

`f(x) = \lambda e^(-\lambda x) , x\geq 0`

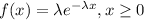
In order to find the cdf we need to do the following integral:

`F(x) = \lambda \int_0^(\infty) e^(-\lambda x) dx= -e^(-\lambda x) \Big|_0^(\infty) = 1- e^(-\lambda x) \`

Part b

Assuming that
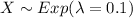`X \sim Exp(\lambda =0.1)`, then the density function is given by:

`f(x) = 0.1 e^(-0.1 x) dx , x\geq 0`

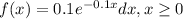
And for this case we want this probability:

`P(10 < X<20) = \int_(10)^(20) 0.1 e^(-0.1 x) dx = -e^(-0.1 x) \Big|_(10)^(20)`

And evaluating the integral we got:

`P(10 < X<20)=e^(-0.1*10) -e^(-0.1*20)=0.368-0.135=0.233`