Question

On the 1st January 2014 Carol invested some money in a bank account.

The account pays 2.5% compound interest per year.
On 1st January 2015 Carol withdrew £1000 from the account.
On 1st January 2016 she had £23517.60 in the account.
Work out how much Carol originally invested in the account.

Answer 1

£23360

Explanation:

She started with x.

After 1 year, she had 1.025x.

She withdrew £1000, so now she has 1.025x - 1000.

Then it earned interest for 1 year and ended up as 1.025(1.025x - 1000).

The actual amount of money was £23 517.60.

Therefore,

1.025(1.025x - 1000) = 23517.60

1.025x - 1000 = 22 944

1.025x = 23 944

x = 23 360

Her original deposit was £23 360

Answer 2

`\large \boxed{\text{\pounds 23 360.00}}`

Explanation:

The formula for the accrued amount from compound interest is

`A = P \left(1 + (r)/(n)\right)^(nt)`

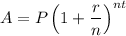
1. Amount in account on 1 Jan 2015

(a) Data:

a = £23 517.60

r = 2.5 %

n = 1

t = 1 yr

(b) Calculations:

r = 0.025

`\begin{array}{rcl}23517.60 & = & P\left (1 + (r)/(n)\right)^(nt)\\\\& = & P\left (1 + (0.025)/(1)\right)^(1*1)\\\\& = & P (1 + 0.025)\\ & = & 1.025 P\\P & = & (23517.60 )/(1.025) \\\\& = & 22 944.00 \\\end{array}`

The amount that gathered interest was £22 944.00 but, before the interest started accruing, Carol had withdrawn £1000 from the account.

She must have had £23 944 in her account on 1 Jan 2015.

(2) Amount originally invested

(a) Data

A = £23 944.00

`\begin{array}{rcl}23 944.00 & = & 1.025 P\\P & = & (23 944.00 )/(1.025) \\\\& = & \mathbf{23 360.00} \\\end{array}\\\text{Carol originally invested $\large \boxed{\textbf{\pounds23 360.00}}$ in her account.}`

3. Summary

1 Jan 2014 P = £23 360.00

1 Jan 2015 A = 23 944.00

Withdrawal = -1 000.00

P = 22 944.00

1 Jan 2016 A = £23 517.60