Question

Triangle ABC has vertices A(0,0) B(3,3) C(6,0) find the orthcenter of triangle abc

Answer 1

(3, 0)

Explanation:

The orthocentre of a triangle is the intersection point of the three perpendicular bisectors of the three sides.

A perpendicular bisector cuts a line in half and meets it at 90°.

You need to know the midpoint and slope for at least two of the sides.

Midpoint formula:
`M = ((x_(2)+x_(1))/(2) ,(y_(2)+y_(1))/(2))`

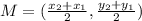
Slope formula:
`m = (y_(2) - y_(1))/(x_(2) - x_(1))`

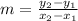
When a line a perpendicular to another, its slope is the negative reciprocal.

The midpoint of the side is a point on the bisector.

Let's focus on the side AB.

Info set 1: A(0,0) x₁ = 0 y₁ = 0

Info set 2: B(3,3) x₂ = 3 y₂ = 3

Find the midpoint:

`M = ((x_(2)+x_(1))/(2) ,(y_(2)+y_(1))/(2))`

`M = ((3+0)/(2) ,(3+0)/(2))`

`M = ((3)/(2) ,(3)/(2))`

`M = (1.5, 1.5)`

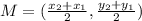
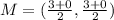
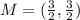
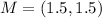
Find the slope:

`m = (y_(2) - y_(1))/(x_(2) - x_(1))`

`m = (3 - 0)/(3 - 0)`

`m = (3)/(3)`

`m = 1/1`

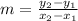
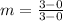
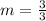
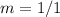
To find the perpendicular line's slope, find the negative reciprocal. (Switch the top and bottom of the slope in fraction form, then change the negatuve/positive)

⊥m = -1/1

⊥m = -1

Find the equation of ⊥AB using m = -1 and (1.5, 1.5).

Substitute into the equation of a line.

y = mx + b

1.5 = -1(1.5) + b

1.5 = -1.5 + b Adding 1.5 to both sides

b = 3

⊥AB : y = -x + 3

Do the same for side AC

Info set 1: A(0,0) x₁ = 0 y₁ = 0

Info set 2: C(6,0) x₂ = 6 y₂ = 0

Find the midpoint:

`M = ((x_(2)+x_(1))/(2) ,(y_(2)+y_(1))/(2))`

`M = ((6+0)/(2) ,(0+0)/(2))`

`M = ((6)/(2) ,(0)/(2))`

`M = (3, 0)`

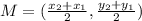
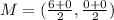
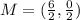
Find the slope:

`m = (y_(2) - y_(1))/(x_(2) - x_(1))`

`m = (0 - 0)/(6 - 0)`

`m = (0)/(6)`

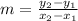
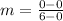
m = 0 This means the line is horizontal

A line perpendicular would be vertical. (⊥m = ∞)

Vertical lines are written in the form y=x, where x is the x-intercept.

Since the midpoint is (3, 0), the midpoint is 3.

⊥AC : y = 3

The intersection point of y = 3 and y = -x + 3 is the orthcentre.

Substitute y for 3 in the equation y = -x + 3

y = -x + 3

3 = -x + 3

x = 0

The orthocentre is (3, 0).

Check for the other line ⊥BC.

Info set 1: B(3,3) x₁ = 3 y₁ = 3

Info set 2: C(6,0) x₂ = 6 y₂ = 0

Find the midpoint:

`M = ((x_(2)+x_(1))/(2) ,(y_(2)+y_(1))/(2))`

`M = ((6+3)/(2) ,(0+3)/(2))`

`M = ((9)/(2) ,(3)/(2))`

`M = (4.5 ,1.5)`

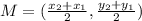
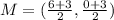
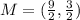
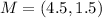
Find the slope:

`m = (y_(2) - y_(1))/(x_(2) - x_(1))`

`m = (0- 3)/(6 - 3)`

`m = (-3)/(3)`

`m = (-1)/(1)`

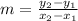
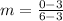
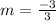
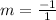
Find its negative reciprocal

⊥m = 1

Substitute slope and the point into the equation of a line

y = mx + b

1.5 = 1(4.5) + b

1.5 = 4.5 + b

b = -3

⊥BC : y = x - 3

Substitute the orthocentre (3,0)

y = x - 3

0 = 3 - 3

0 = 0

LS = RS

Therefore the orthocentre is (3, 0)