Answer:
81.9756 m/s
16.8 m
4.8795 Hz
Step-by-step explanation:
m = Mass of string = 0.12 kg
L = Length of string = 8.4 m
T = Tension on string = 96 N
Linear density is given by
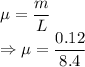
Spee of the wave is given by
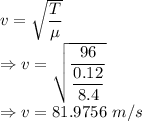
The speed of the waves on the string is 81.9756 m/s
Wavelength is given by
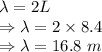
The longest possible wavelength is 16.8 m
Frequency is given by
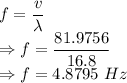
The frequency of the wave is 4.8795 Hz