Question

A string fixed at both ends is 8.40 m long and has a mass of 0.120 kg. It is subjected to a tension of 96.0 N and set oscillating.

(a) What is the speed of the waves on the string?
(b) What is the longest possible wavelength for a standing wave?
(c) Give the frequency of that wave.

Answer 1

81.9756 m/s

16.8 m

4.8795 Hz

Step-by-step explanation:

m = Mass of string = 0.12 kg

L = Length of string = 8.4 m

T = Tension on string = 96 N

Linear density is given by

`\mu=(m)/(L)\\\Rightarrow \mu=(0.12)/(8.4)`

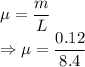
Spee of the wave is given by

`v=\sqrt{(T)/(\mu)}\\\Rightarrow v=\sqrt{(96)/((0.12)/(8.4))}\\\Rightarrow v=81.9756\ m/s`

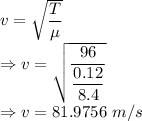
The speed of the waves on the string is 81.9756 m/s

Wavelength is given by

`\lambda=2L\\\Rightarrow \lambda=2* 8.4\\\Rightarrow \lambda=16.8\ m`

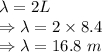
The longest possible wavelength is 16.8 m

Frequency is given by

`f=(v)/(\lambda)\\\Rightarrow f=(81.9756)/(16.8)\\\Rightarrow f=4.8795\ Hz`

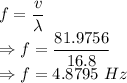
The frequency of the wave is 4.8795 Hz