Answer:
a) 0 Nm b) mgL/2 Nm counterclockwise
Step-by-step explanation:
Before we even begin answering the question, we have to appreciate the fact that the weight of the constant density symmetrical rigid objects is considered to be acting from its geometrical center, which we will call the center of mass. If the clock arm is considered to be rectangular , rigid and constant density(assumed, since this is a high school question) we can proceed with our analysis. We also note that the torque on the arm are given by,
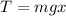
where m is the total mass of the arm , x is the horizontal distance(perpendicular to the direction of force) of the center of mass of the arm from the center of the clock and g is the acceleration due to gravity. Also let L be the length of the hour arm.
In part a) the horizontal distance of the center of mass of the arm from the center of the clock would be zero since at noon the center of mass of the clock arm is right above the center of the clock. So x = 0 , hence T = 0 Nm.
in part b) the horizontal distance between the center of mass of the arm and the center of the clock is L/2 , where L is the length of the hour arm , but the weight acts from half that distance since the weight of the object is considered to be acting from the geometrical center of the object which in this case is L/2 distance away from the center of the clock. So plugging into the above equation we get T = mg*(L/2) Nm, the force acting downwards from the left since the arm is pointing at 9:00 , which will result in a counter clockwise torque. So T=mgL/2 Nm counter clockwise is the Torque due to the hour arm.
If you already know calculus you can check the answer to part b) by evaluating the integral,
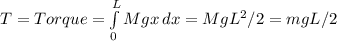
where M is the mass per unit length of the arm. m is the total mass given by m=ML.