Answer:
![(dy)/(dx) = e^{x^(2) } ( (1)/(x) + 2x ln2x )</strong></p><p><strong>Step-by-step explanation:</strong></p><p>Let Given function<strong> (y) = [tex]e^{x^(2)} ln2x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/p51oyq6vamb2cw32omewa2mkfpylkq6r31.png)
If we differentiate this function with respect to x -
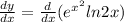
As we know that-
\frac{d}{dx} ( I × II ) = I × \frac{d}{dx} ( II ) + II × \frac{d}{dx} (I)
[tex]\frac{dy}{dx} = e^{x^{2} } \frac{d}{dx} ( ln2x ) + ln2x \frac{d}{dx} ( e^{x^{2} })
[tex]\frac{dy}{dx} = e^{x^{2} } \frac{1}{2x} × 2 + ln2x × e^{x^{2} } × 2x
[tex]\frac{dy}{dx} = e^{x^{2} } \frac{1}{x} + ln2x × e^{x^{2} } × 2x
[tex]\frac{dy}{dx} = e^{x^{2} } ( \frac{1}{x} + 2x ln2x )