Question

Compute the internal rate of return for the cash flows of the following two projects (Do not round intermediate calculations. Enter your answers as a percent rounded to 2 decimal places, e.g., 32.16.): Year Project A Project B 0 –$ 11,300 –$ 8,900 1 4,400 2,400 2 5,200 6,500 3 4,000 3,600

Answer 1

The internal rate of return for the cash flows of Project A is near about .10 and Project B is near about .18.

Step-by-step explanation:

Computing the internal rate of return (IRR) for the cash flows.

IRR=
`(cash\ flows)/((1+r)^(t) ) -intital\ investment= 0`

Cash flows= Cash flows in the time period.

r= Discount rate.

t= Time period.

Project A:

Lets assume a minimum rate of return at which net present value of all cash flow from project equal zero. we will start with IRR= .10.

=
`(\$ 4400)/((1+.10)^(1) ) + (\$ 5200)/((1+.10)^(2) ) + (\$ 4000)/((1+.10)^(3) )- \$ 11300`

=
`\$ 4000+\$ 4297+\$ 3005-\$ 11300`

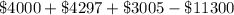
∴ IRR at .10 is giving return which is very close to getting net present value (NPV) is equal to zero.

Project B.

As initial investment is less in project B, so lets take IRR as .15 first to check if it is giving NPV equal to zero.

=
`(\$ 2400)/((1+.15)^(1) ) + (\$ 6500)/((1+.15)^(2) ) + (\$ 3600)/((1+.15)^(3) )- \$ 8900`

=
`(\$ 2086+\$ 4914.93+\$ 2367)-\$ 8900`

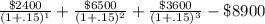
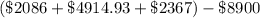
Opening parenthesis.

=
`\$ 9367.93-\$ 8900=\$ 467.93`

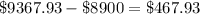
Here we are getting higher NPV, therefore we will check another IRR. Lets take .18.

=
`(\$ 2400)/((1+.18)^(1) ) + (\$ 6500)/((1+.18)^(2) ) + (\$ 3600)/((1+.18)^(3) )- \$ 8900`

=
`(\$ 2033.89+\$ 4668+\$ 2191)-\$ 8900`

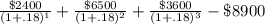
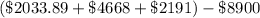
Opening parenthesis.

=
`\$ 8892.96-\$ 8900=\$ 7.04`

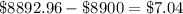
IRR at .18 for project B is giving return which is very close to getting net present value (NPV) is equal to zero.

∴ The internal rate of return for the cash flows of Project A is near about .10 and Project B is near about .18