Question

The fox population in a certain region has a relative growth rate of 4% per year. It is estimated that the population in year 2000 was 17900.(A.) Find a function that models the population t years after 2000 (t=0 for 2000) and (B.) Use the function from part A to estimate the fox population in the year 2008.------> answer must be an integer.

Answer 1

a)
`P(t) = 17900e^(0.04t)`

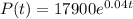
b) The population estimated in 2008 is of 24651.

Explanation:

The population growth model may be given by the following exponential function:

`P(t) = P_(0)e^(rt)`

In which P(t) is the population after t years,
`P_(0)` is the initial population and r is the growth rate.

(A.) Find a function that models the population t years after 2000 (t=0 for 2000)

We have that:

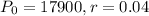`P_(0) = 17900, r = 0.04`. So

`P(t) = P_(0)e^(rt)`

`P(t) = 17900e^(0.04t)`

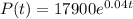
(B.) Use the function from part A to estimate the fox population in the year 2008.

2008 is 8 years after 2000. So:

`P(8) = 17900e^(0.04*8) = 24650.5`

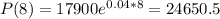
The population estimated in 2008 is of 24651.