Question

Sales at a fast-food restaurant average $6,000 per day. The restaurant decided to introduce an advertising campaign to increase daily sales. To determine the effectiveness of the advertising campaign, a sample of 49 days of sales were taken. They found that the average daily sales were $6,300 per day. From past history, the restaurant knew that its population standard deviation is about $1,000. If the level of significance is 0.01, have sales increased as a result of the advertising campaign? Multiple Choice

A. Reject the null hypothesis and conclude that the mean is equal to $6,000 per day.
B. Fail to reject the null hypothesis.
C. Reject the null hypothesis and conclude the mean is lower than $6,000 per day.
D. Reject the null hypothesis and conclude the mean is higher than $6,000 per day.

Answer 1

Option B) Fail to reject the null hypothesis.

Explanation:

We are given the following in the question:

Population mean, μ = $6,000

Sample mean,
`\bar{x}` = $6,300

Sample size, n = 49

Alpha, α = 0.01

Population standard deviation, σ = $1,000

First, we design the null and the alternate hypothesis

`H_(0): \mu = 6000\text{ dollars per week}\\H_A: \mu > 6000\text{ dollars per week}`

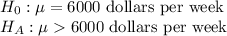
We use one-tailed(right) z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

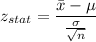
Putting all the values, we have

`z_(stat) = \displaystyle(6300 - 6000)/((1000)/(√(49)) ) = 2.1`

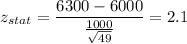
Now,
`z_(critical) \text{ at 0.01 level of significance } = 2.33`

Since,

`z_(stat) < z_(critical)`

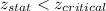
We fail to reject the null hypothesis and accept the null hypothesis. Thus, we conclude that sales have not increased as a result of the advertising campaign

Option B) Fail to reject the null hypothesis.