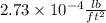Answer:
Complete Question
![u=U_(max) [0.5(y)/(h)-3(y^(2) )/(h) ]](https://img.qammunity.org/2020/formulas/engineering/college/ggdkrqdivyn3s08irtdgxl9bpay9ft2pl3.png)
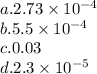
Answer
τ at y = 0 =
Step-by-step explanation:
The work function is given as
![u=U_(max) [0.5(y)/(h)-3(y^(2) )/(h) ]](https://img.qammunity.org/2020/formulas/engineering/college/ggdkrqdivyn3s08irtdgxl9bpay9ft2pl3.png)
where
Umax = maximum velocity = 5 fps(foot per second)
h= depth (h) of the storm water =
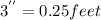
Shear stress on the ground surface = ? τ=
![u=U_(max) [0.5(y)/(h)-3(y^(2) )/(h) ]](https://img.qammunity.org/2020/formulas/engineering/college/ggdkrqdivyn3s08irtdgxl9bpay9ft2pl3.png)
considering
![u=U_(max) [0.5(y)/(h)-3(y^(2) )/(h) ]](https://img.qammunity.org/2020/formulas/engineering/college/ggdkrqdivyn3s08irtdgxl9bpay9ft2pl3.png)
Considering
τ =
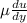
Taking derivatives
![(du)/(dy)=\mu_(max) [(0.5)/(h) -(3)/(h^(2) ) *2y]](https://img.qammunity.org/2020/formulas/engineering/college/60pc5d0hbuneybap9buqjke6xh3lusxjh7.png)
At y = 0
![(du)/(dy)=5[(0.5)/(0.25) ] =10](https://img.qammunity.org/2020/formulas/engineering/college/ro5k6d42ouubljjcaaf7iiaknv6vah8m7z.png)
therefore
τ at y = 0 =
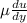
=
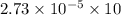
τ at y = 0 =